
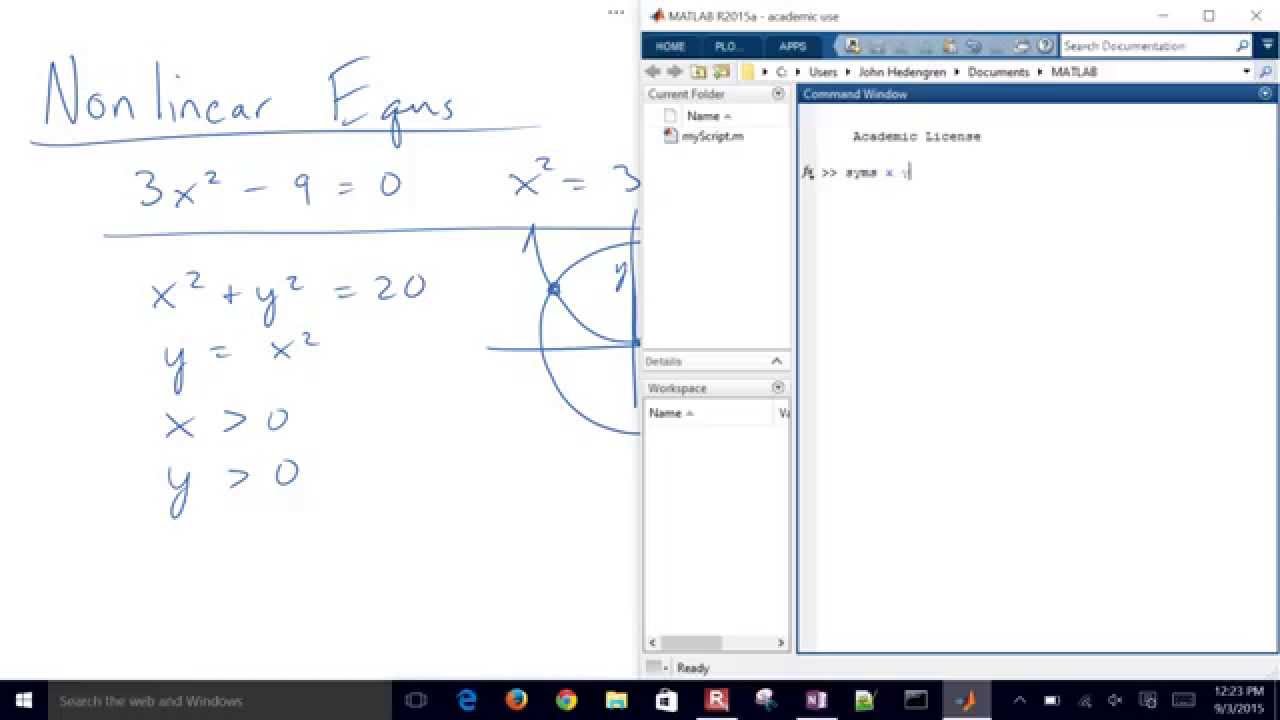
Although the present question is a very small problem and won't be any trouble doing in Matlab using symbolic calculations as well, but still it is a good practice to do a problem numerically in matlab and symbolically in mathematica/maple etc. criteria details ans 1.0e-08 0.5447 0.1506 0.0561 0.5447 0.1506 0. Matlab is very inappropriate and slow for symbolic problem solving. You can use the following function to get the points on an ellipse and then plot those points.
The two more popular and versatile algorithms provided in MATLAB are fzero and fsolve. fsolve stopped because the relative size of the current step is less than the default value of the step size tolerance squared, but the vector of function values is not near zero as measured by the default value of the function tolerance. Therefore we write a function whose inputs and outputs are: Inputs: r1,r2: major and minor axis respectively C: center of the ellipse (cx,cy) Output: x,y: points on the circumference of the ellipse. Working of fsolve in Matlab with Syntax and Examples. It solves the equations and returns a vector value for the objective function entered in the syntax.

It's easy to get around this once you know it's happening. function F paramfun (x,c) F 2x (1) + x (2) - exp (cx (1)) -x (1) + 2x (2) - exp (cx (2)) end Solve a Problem Structure Create a problem structure for fsolve and solve the problem. MATLAB provides several algorithms for solving nonlinear equations. In Matlab, fsolve is the function that is used to solve nonlinear equations. Why should that imply that our search space is complex? These issues are independent. If a function returns complex values and we would like to find a point where it's zero, we would effectively be setting two constraints on the input variables using just one equation. In this video tutorial, Solving system of nonlinear equations has been reviewed and implemented using fsolve in MATLAB. The other idea, to use a change of variables, could also work. Also, it uses the same input format and algorithms, with the only conspicuous difference being that it doesn't include the "trust region dogleg" method, that fsolve(.) does. Now, there is no way documented on fsolve's help page of bounding the domain, but checking this answer, it turns out that there is a function lsqnonlin(.), which is very similar to fsolve(.), except that it does allow us to specify lower and upper bounds on the variables. Or adjust the function to not return complex numbers. In the example from the question this probably happens because fsolve(.) calls the anonymous function with x(2) being negative at some point, which the function then raises to the power of 0.1, producing a complex output.Īnyway, the two suggestions in the above post are to Please find the below syntaxes that are used while dealing with the fsolve function: 1. I don't see this as logical behaviour, but that's the way it works. In Matlab, the fsolve function is used to get the solutions of any nonlinear equations that are defined or declared in the environment. If you don't want to mess with the builtin matlab code, you can save createOptionFeedback.m in the same path as your program, and it will override the built in function.This post by MathWorks Support says that if the objective function ever returns a complex number, then fsolve(.) automatically switches to treat the input variable as being complex as well. My particular problem went from a 15 minute running time to about 2-3 minutes. If you edit the file createOptionFeedback.m and comment out line 19 (in r2009b), it will save a _ton_ of computation time! I tracked it down to the fact that levmar is repeatedly calling optimset(options), in order to check that the options you supplied to the algorithm are valid. I realize this is a bit of a late reply, but I also had this problem. > optionFeedback = createOptionFeedback(options) > call inside the optionFeedback = createOptionFeedback(options) function that in turn is called by the fsolve function according to the profiler the line After profiling, I found that the main culprit is the One of my programs, that runs in about 100 seconds in Matlab r2009a, runs now in about 200 seconds in r2009b.


 0 kommentar(er)
0 kommentar(er)
